In this case, the truth values for ~(p∧q) and ~p∨~q are exactly the same, so we can conclude that the two statements are equivalent ~(p∧q)≡~p∨~qSo, if we ever encounter ~(p∧q), we can replace it with ~p∨~q without changing the logical meaning of the statement!Now let's try comparing two more complex statements to see if they are equivalentDoes the conclusion must be true?

Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download
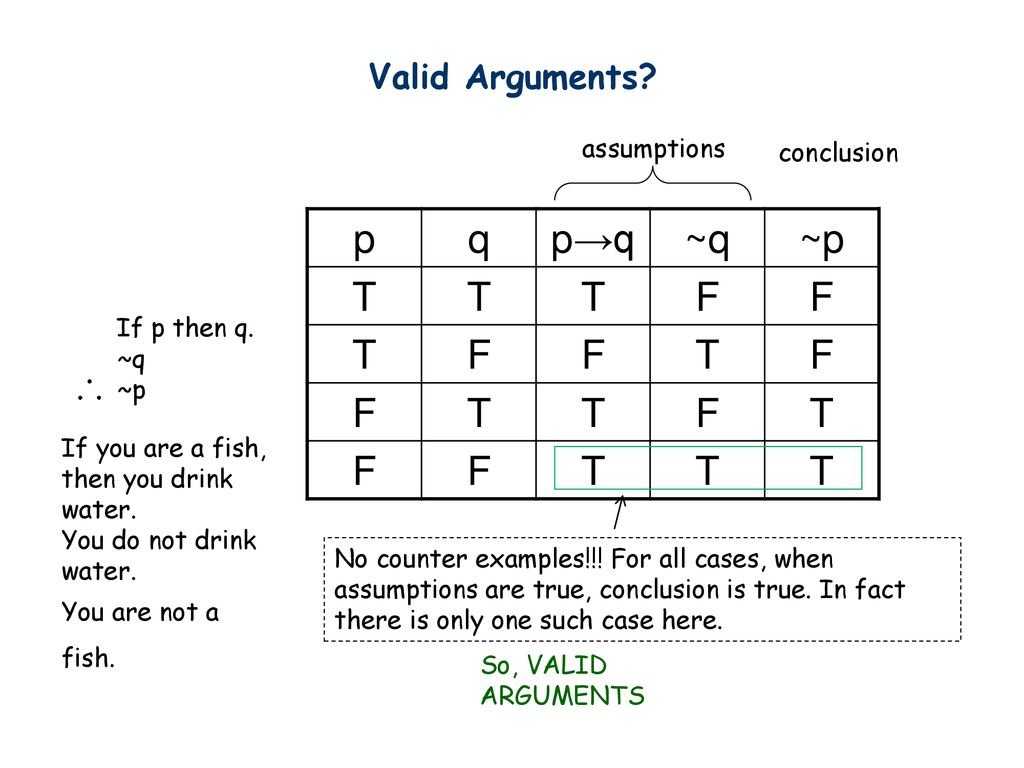
If p then q q therefore p example
If p then q q therefore p example-P q p → q ∼ q ∼ p T T T F F T F F T F F T T F T → F F T T T In this case there is only one critical row to consider, and its truth value it true Hence this is a valid argument Result 22 (Generalization) Suppose p and q are statement forms Then the following arguments (called generalization) are valid p p∨q q p∨ q Result 23And if p then r;




Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download
Addition If P is a premise, we can use Addition rule to derive $ P \lor Q $ $$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ ExampleTherefore p is true Conjunction p,q ∴ (p∧q) p and q are true separately;For example, if the claims P and Q express the same proposition, then the argument would be trivially valid, as it would beg the question In everyday discourse, however, such cases are rare, typically only occurring when the "ifthen" premise is actually an " if and only if " claim (ie, a biconditional / equality )
To say that q is a "necessary component" of p is to mean that if one has p one must also have q, that is "if p then q" For example, "an engine is a necessary component of a functioning automobile" means that if one has a functioning car then one has an engine, rather than if one has an engine then one has a functioning car So, Morris' argument is as follows If you believe inAs far as I understand, If p then Q means " if P is true, Q has to be true Any other case, I don't know " So, from what I understand, the first 2 rows of the truth table state that " If P is true and Q is true, the outcome is correct and If P is true and Q is false,P ^ q is trueif and only if p and q are both true Example Alice is tall AND slim Truth table for conjunction p q p ^ q T T T T F F F T F F F F c Xin He (University at Buffalo) CSE 191 Discrete Structures 11 / 37 Disjunction Another binary operator isdisjunction _ , which corresponds toor, (but is slightly different from common use)
上 if p then q if q then r therefore if p then r If p then q or r ;False The key to identifying an argument in context is to first identify the conclusion, then look for the premises a True b False This classic argument "The Bible says that God exists;Is P and Q 2 is P and Q a n is P and Q Conclusion (generalization) All Ps are Qs An argument is strong if and only if the premises provide significant support for the conclusion That is, if the premises were true, then it is likely that the conclusion is true Another way of putting this is that the truth of the premises




In Praise Of Rationality The New York Times




Philosophy Logic And Logical Arguments Ppt Video Online Download
Therefore they are true conjointly Addition p ∴ (p∨q) p is true;Example If we turn of the water in the shower, then the water will stop pouring If we call the first part p and the second part q then we know that p results in q This means that if p is true then q will also be true This is called the law of detachment and is noted $$\leftIt consists of the antecedent (the part introduced by the word if) and the consequent (the part introduced by the word then) Consequent The part of a conditional statement (If p, then q) introduced by the word then Deductive Argument




In Praise Of Rationality The New York Times




Is P Land P To Q To Q A Tautology Mathematics Stack Exchange
The final (or concluding) statement in an argument Symbol for "therefore", normally used to identify the conclusion of an argument Latin for "method of affirming" A rule of inference used to draw logical conclusions, which states that if p is true, and if p implies q ( pq ), then q is trueIf I have a college degree, then I am not lazy (p →~ q) I don't have a college degree )(~ p Therefore, I am lazy q Hypothesis )((p →~ q)∧~ p Conclusion q Argument in symbolic form (( p →~ q)∧~ p) →q To test to see if the argument is valid, we take the argument in symbolic form and construct a truth tableIf p→q is a conditional statement, then (1) q→p is called converse of p→q (2) ¬q→¬p is called contrapositive of (3) ¬p→¬q is called inverse of p→q EXAMPLE p Ram is a computer science student q Ram study DBMS p→q If Ram is a computer science student, then the will study DBMS




Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero




Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero
One way to write the conditional is "if p, then q" Thus, if you know p, then the logical conclusion is q Consider this as you review the following truth table Why is this true?(pVq) V (~p^q) → q p q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18 (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a6 CHAPTER 1 LOGIC 14 Converse and Contrapositive The converse of the implication p!qis q!p The example above shows that an implication and its converse can have di erent truth values, and




Cse15 Discrete Mathematics 01 30 17 Ppt Download



Propositional Logic Ppt Download
Solution In Example 1, the sentence, "I do my homework" is the hypothesis and the sentence, "I get my allowance" is the conclusion Thus, the conditional p q represents the hypothetical proposition, "If I do my homework, then I get an allowance" However, as you can see from the truth table above, doing your homework does not guarantee that you will get an allowance!If p then q;Therefore either not p or not r Simplišcation (p∧q) ∴ p p and q are true;




Ppt Logic Powerpoint Presentation Free Download Id




Conditional Statements If P Then Q Youtube
The argument is valid modus ponens inference rule We cannot conclude that the conclusion is true, since one of its premises, p 2 > 3 2, is false Indeed, in this case the conclusion is Conditional statement if she studies math (p), then she will find a good job (q) This is of the type If p, then q q unless p She finds a good job unless she does not study math Here q is true only is ~p (not p) is false If ~p is true then q will become false Hope this helped!Therefore, God exists" is an example of begging the question a True




Evaluating Philosophical Claims And Theories Ppt Video Online Download




Converse Inverse And Contrapositive Of Conditional Statement Chilimath
Therefore if p is trueWays in which the propositions may fail to be equivalent Here is another example Example 232 Show (p!q) is equivalent to p^q Solution 1 Build a truth table containing each of the statements p q q p!q (p!q) p^q T T F T F F T F T F T T F T F T F F F F T T F F Since the truth values for (p!q) and p^qare exactly the same for all possible5月 30, 21 Result 26 (Transitivity) Suppose p, q and r are statement forms Then the following argument (called transitivity) is valid p → q q → r p → r Result 27 (Proof by Division into Cases) Suppose p, q and r are




Reasoning And Critical Thinking Ppt Download




Pdf Rules Of Logical Inference Dr Jason J Campbell Academia Edu
P then q" or "p implies q", represented "p → q" is called a conditional proposition For instance "if John is from Chicago then John is from Illinois" The proposition p is called hypothesis or antecedent, and the proposition q is the conclusion or consequent Note that p → q is true always except when p is true and q is falseTherefore, the argument must be valid 5 Valid We can test for validity by substituting statement variables into the argument If we do the substitution, we get If p, then q Not q Therefore, not p Upon inspection, we find that this is one of the common patterns of valid inference discussed above—modus tollensGiven "p implies q", there are two possibilities We could have "p", and therefore "q" (so q is possibility 1)



Math Washington Edu



Www3 Cs Stonybrook Edu
Specifically given two propositions p and q, then the resulting proposition 'p or q' means 'p or q' is a true proposition even when both p and q are true An example would be, "John is a student or John is a father' If John is both a student and a father, then the entire sentence is still true The phrase 'exclusive or' means 'p or q but notFor example, in terms of propositional logic, the claims, "if the moon is made of cheese then basketballs are round," and "if spiders have eight legs then Sam walks with a limp" are exactly the same They are both implications statements of the form, P → Q P → Q 🔗NotQ 3 Therefore, Q 3 Therefore, P Two Common Invalid Argument Forms Affirming the Consequent 1 If P, then Q 2 Q 3 Therefore, P Denying the Antecedent 1 If P, then Q 2 notP 3 Therefore, notQ




Ppt 22c 19 Discrete Structures Logic And Proof Powerpoint Presentation Id



Nyu Edu
So, in the Form given above, the consequent is "q" For example, in the statement "if today is Tuesday, then I have logic class", "I have logic class" is the consequent To affirm the consequent is, of course, to claim that the consequent is true Thus, affirming the consequent in the example would be to claim that I have logic classIf I use my turning signal while driving in MO then I will go to jail Disjunctive Syllogism Form p or q not p therefore q Disjunctive Syllogism ( valid and sound) I will eat either yogurt and granola or a bagel and cream cheese for breakfast tomorrowP is called the hypothesis and q is called the conclusion For instance, consider the two following statements If Sally passes the exam, then she will get the job If 144 is divisible by 12, 144 is divisible by 3



6 Conditional Derivations A Concise Introduction To Logic




Cse261 Chapter1 Flashcards Quizlet
The Converse of a Conditional Statement For a given the conditional statement {\color{blue}p} \to {\color{red}q}, we can write the converse statement by interchanging or swapping the roles of the hypothesis and conclusion of the original conditional statement Therefore, the converse is the implication {\color{red}q} \to {\color{blue}p} Notice, the hypothesis \large{\color{blue}p} of theBut either not q or not s;In conditional statements, "If p then q" is denoted symbolically by "p q";




Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download




Autodidacticism
Answer (1 of 6) The easiest way is by recalling that the contrapositive has the same truth value as the original statement So since P implies Q is true then not Q implies not P is also true However, the question remains how do we know that the contrapositive is true given the statement is truIs true if either P is true or Q is true (or both remember that we're using "or" in the inclusive sense) It's only false if both P and Q are false Here's the table for logical implication To understand why this table is the way it is, consider the following example "If you get an A, then I'll give you a dollar"2 then (p 2)2 > (3 2) 2 We know that p 2 > 3 2 Therefore, (p 2)2 = 2 > (3 2) 2 = 9 4 Is the argument valid?



Stetson Edu
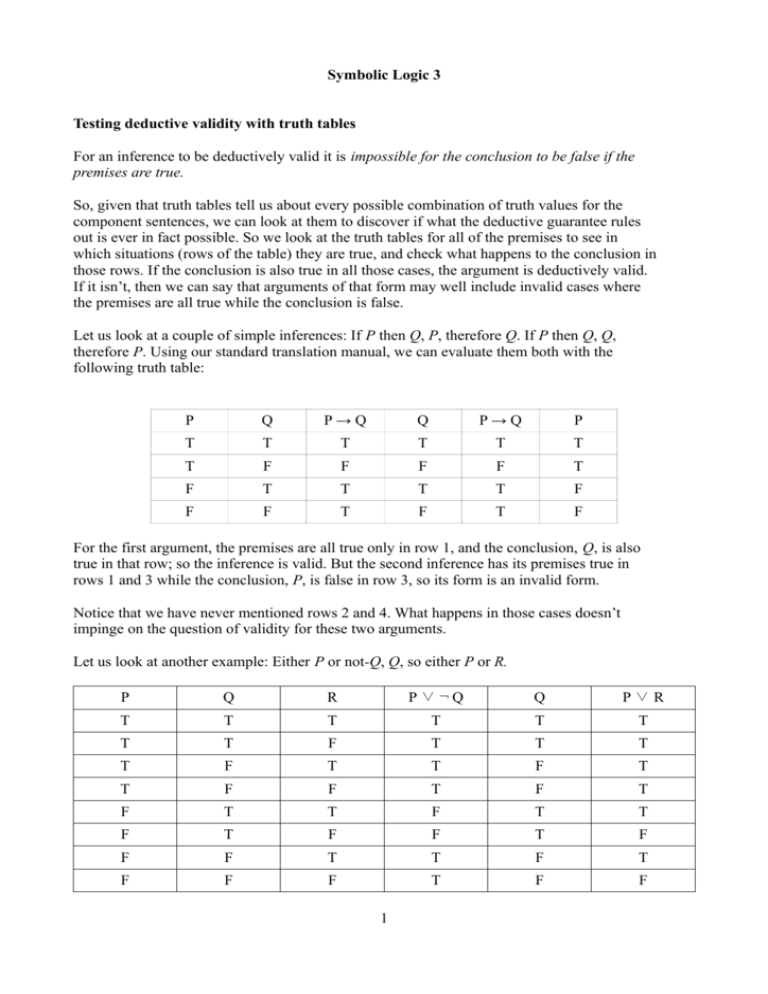



Symbolic Logic 3 Testing Deductive Validity With Truth Tables For An
Solution We want to use the p and q given above as replacements for the p and q in the following argument form (such use is called a replacement instance) If p then q not q Therefore not p Hence we have for (a) If my car is still in the shop then I have to get a ride with a friend I don't have to get a ride with a friend If p, then q Not q Therefore, not p If you don't care, fuck off The Rubber Duck method of debugging We called it the Rubber Duck method of debugging It goes like this 1) Beg, borrow, steal, buy, fabricate or otherwise obtain a rubber duck (bathtub variety) 2) Place rubber duck on desk and inform it you are just going to go over someA conditional statement is a statement of the form "If p, then q" The symbol for this "ifthen" connective is the arrow → That is, the statement "if p, then q" is denoted p→q EXAMPLE 221 Let p represent "You drink Pepsi" Let q represent "You are happy" In this case p→q is the statement "If you drink Pepsi, then you are happy"




Cs 103 Discrete Structures Ppt Download




Philosophy 103 Linguistics 103 Yet Still Even Further
The Bible is true because God wrote it;Rule of inference Modus tollens Definition It has the form If p, then q ∼ q ∴ ∼ p The term modus tollens in Latin means "method of denying" p q p → q ∼ q ∼ p T T T F T F F T F T T F F F T T T Example If Zeus is human, then Zeus is mortal Zeus is not mortal ∴ Zeus is not humanAnd if r then s;



Affirming The Consequent



1
–premises p 1, p 2, , p k –conclusion q then (p 1Ùp 2Ù Ùp k) ®q is a tautology •Ex ( (p®q)Ùp ) ®q is a tautology •Some simple valid argument forms, called rules of inference, are derived and can be used to construct complicated argument formP q r q p r ∴ q aka Disjunction Elimination Corresponding Tautology ((p q) ∧ (r q) ∧ (p r )) q Example Let p be "I will study discrete math" Let q be "I will study Computer Science" Let r be "I will study databases" "If I will study discrete math, then I will study Computer Science"P → q = (~p ∨ q) In the Principia Mathematica, the "=" denotes "is defined to mean" Using this denotation, the above expression can be read "p implies q is defined to mean that either p is false or q is true" The following truth table shows the logical equivalence of "If p




Introduction To Philosophy Smu Fall 16 Tools



6 Conditional Derivations A Concise Introduction To Logic
For example there is no necessary connection between P='22=4' and Q='Washington is the capital of USA',still the inference P > Q is valid,that is always a TRUE implies a TRUE irrespective of the relations between the terms of the propositions P and Q in the russelian (material) definitionOn the other hand there is a necessary one between PTherefore the disjunction (p or q) is true Composition (p → q) (p → r) ∴ (p → (q∧r)) if p then q;




Propositional Logic Conditional Statement If P Then Q




Phil 210 Quiz Logical Fallacy Oneclass




Inductive Reasoning Definition Basing A Conclusion On Specific Examples Examples All Crows Are Black The Sun Will Rise Tomorrow Pdf Free Download



Jstor Org



Osti Gov




Logic Logical Progression Of Thought A Path Others Can Follow And Agree With Begins With A Foundation Of Accepted In Euclidean Geometry Begin With Point Ppt Download




Arguments And Fallacies Argument Clinic N Http Youtu




Ppt Propositional Logic Powerpoint Presentation Free Download Id




Formal Logic The Propositional Calculus Britannica




Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero



Rare Genetic Coding Variants Associated With Human Longevity And Protection Against Age Related Diseases Nature Aging




Review Chapter 8 Deductive Reasoning Deductive Logic Classical By Putting In Proper Form We Will Force Conclusion Standard Form Putting Things In Ppt Download




Cmos Wikipedia



Www2 Math Binghamton Edu




Still More On The Taxonomy Of Logical Fallacies Logic And Critical Thinking Logical Fallacies Critical Thinking



Jstor Org
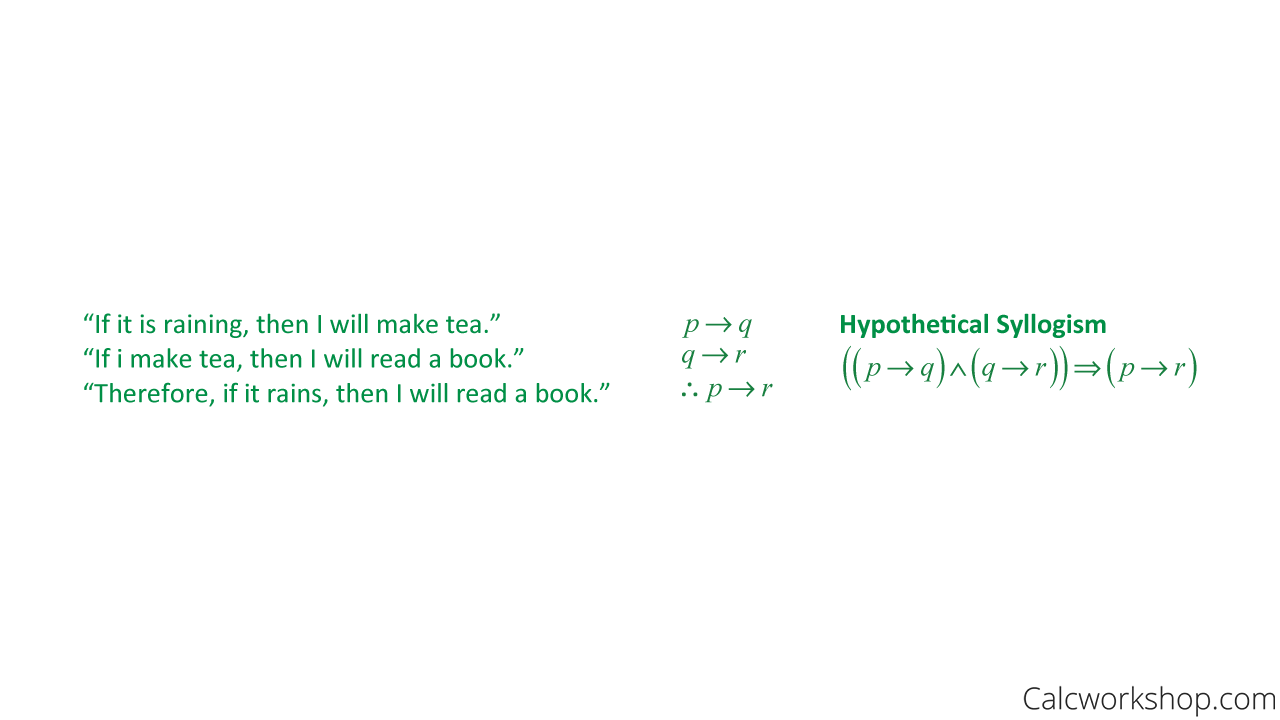



Rules Of Inference Detailed W Step By Step 7 Examples
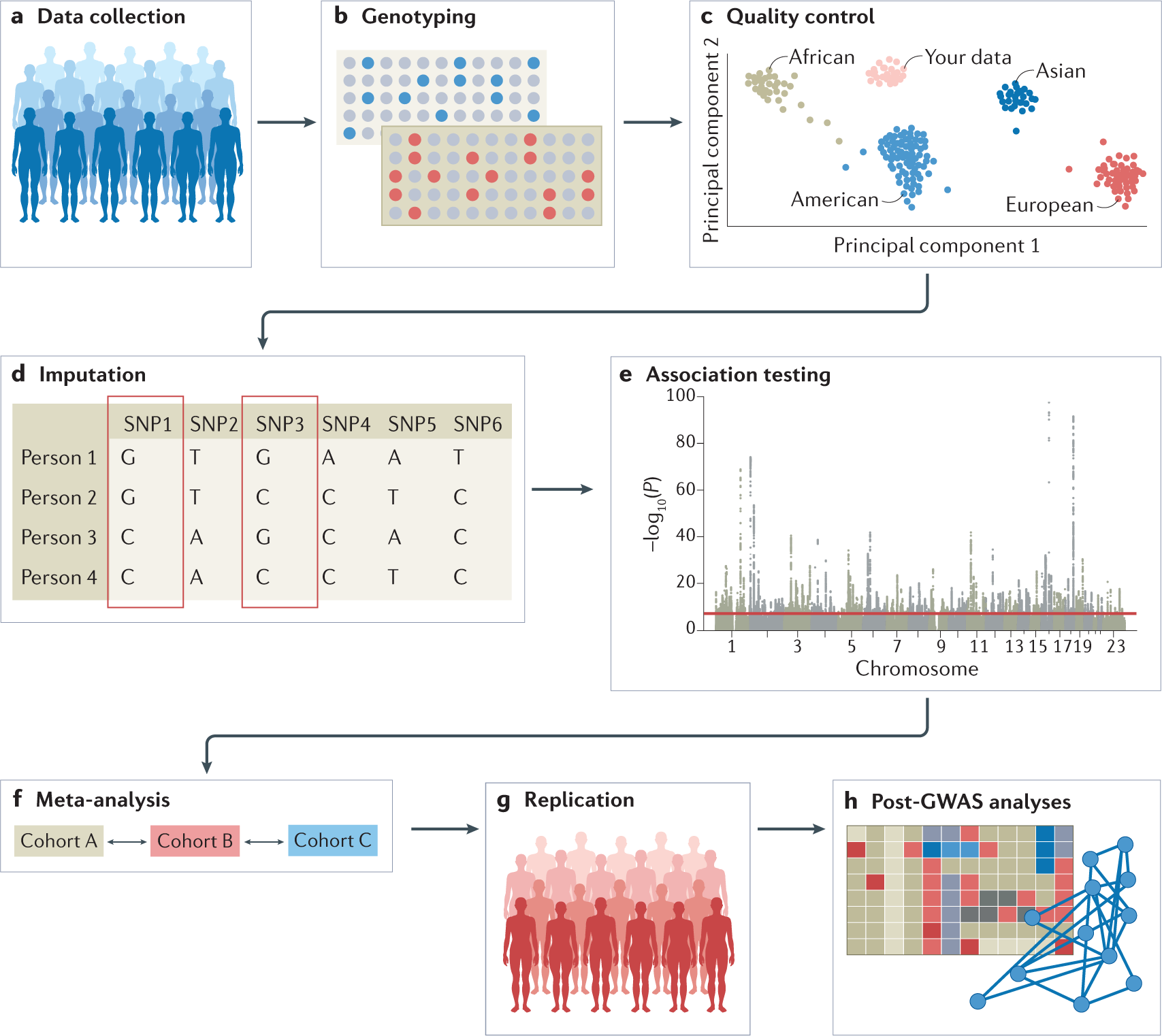



Genome Wide Association Studies Nature Reviews Methods Primers




Logical Fallacies Logical Fallacies Are Statements That May




2 3 Methods Of Proof Ppt Video Online Download




If P To Q Q Vv R Is False Then The Truth Values Of P Q R Are Respectively




Implication œ Conditional Statement P Q P Implies Q If P Then Q




Ppt Abduction And Inference To The Best Explanation Powerpoint Presentation Id




How Does If P Then Q Have The Same Meaning As Q Only If P Mathematics Stack Exchange




Logical Fallacies Logical Fallacies Are Statements That May




1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download



Ocw Mit Edu




Cse261 Chapter1 Flashcards Quizlet




Deductive Validity Truth Preserving The Conclusion Logically Follows From The Premises It Is Logically Impossible For The Premises To Be True And The Ppt Video Online Download



Scholarworks Smith Edu




Logic




1 Valid And Invalid Arguments 2 Definition Of Argument Sequence Of Statements Statement 1 Statement 2 Therefore Statement 3 Statements 1 And 2 Are Ppt Download



Academic Oup Com




In Praise Of Rationality The New York Times




Questions With Answers In Pure Mathematics Science Topic



Siue Edu



People Vcu Edu




C81cog Cognitive Psychology 1 Syllogistic Reasoning Dr Alastair D Smith Room B22 School Of Psychology Ppt Download



Jstor Org



Storm Cis Fordham Edu



Degruyter Com




Argument Quality In Real World Argumentation Trends In Cognitive Sciences



6 Conditional Derivations A Concise Introduction To Logic




End Of Chapter 3 Critical Thinking
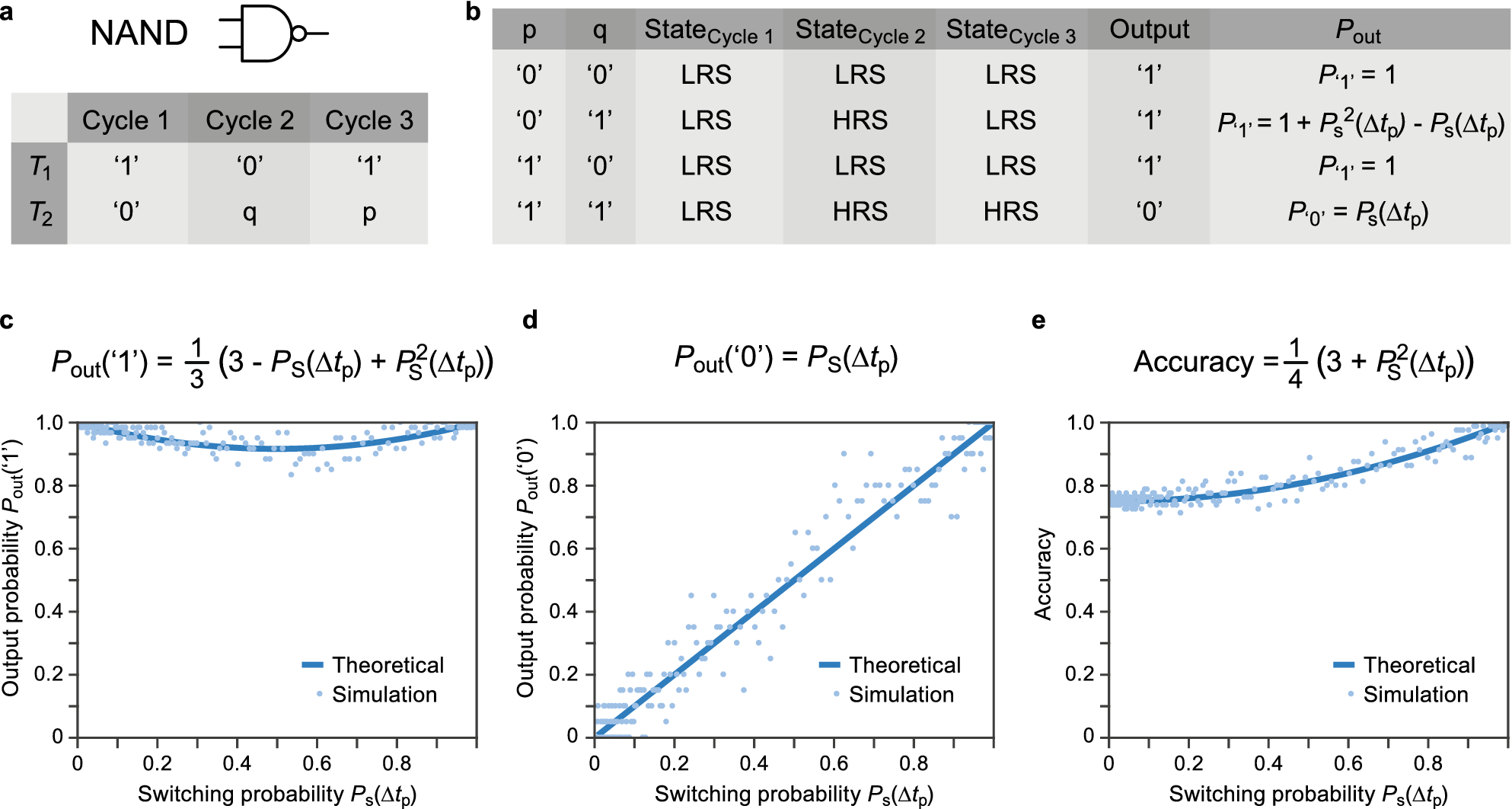



Theory And Experimental Verification Of Configurable Computing With Stochastic Memristors Scientific Reports




Philosophy Logic And Logical Arguments Ppt Video Online Download



Storm Cis Fordham Edu




Converse Inverse And Contrapositive Of Conditional Statement Chilimath
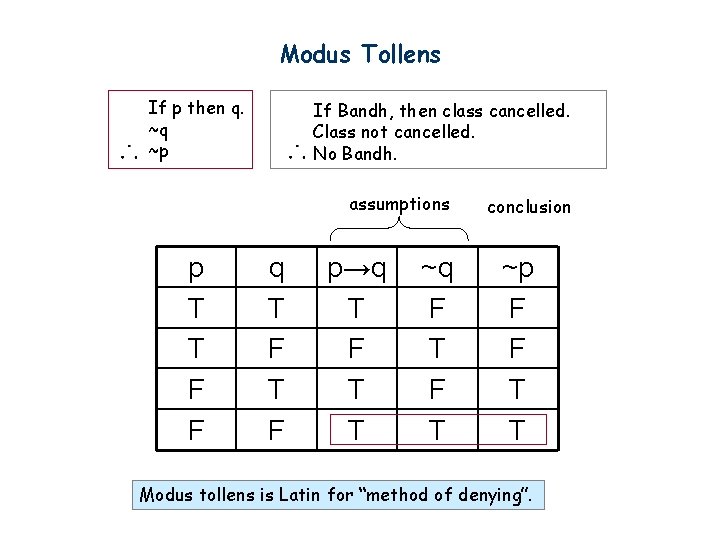



Propositional Logic Conditional Statement If P Then Q




Mathematical Logic Part 2




22 C 19 Discrete Structures Logic And Proof
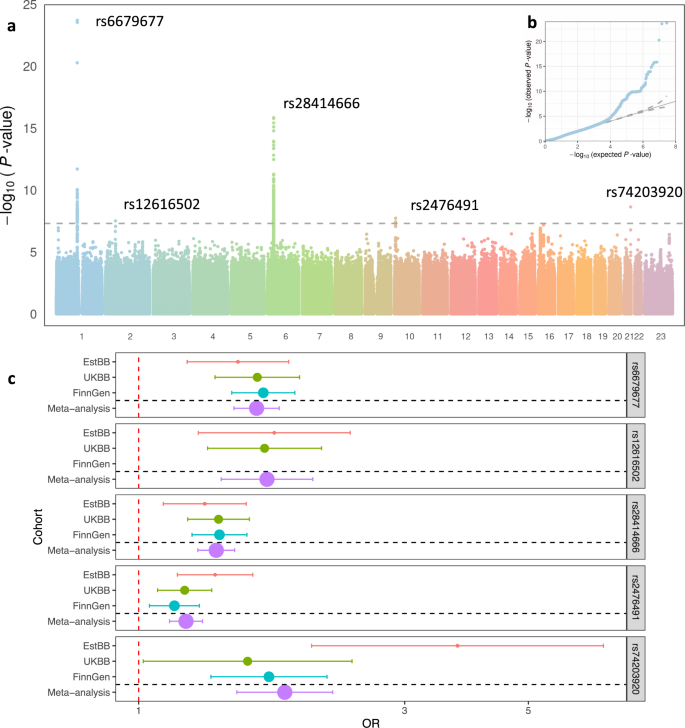



Genome Wide Association Study Identifies Five Risk Loci For Pernicious Anemia Nature Communications



1




1 Introduction To Abstract Mathematics Valid And Invalid Arguments 2 3 Instructor Hayk Melikya Ppt Download



Degruyter Com



Jstor Org




Logical Arguments Modus Ponens Modus Tollens Youtube




Solved Consider The Argument Form P Rightarrow Tilde Q Q Chegg Com
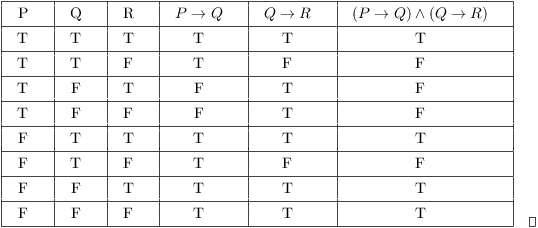



Truth Tables Tautologies And Logical Equivalences




Class Notes For Soc Sci 3a At University Of California Irvine Uc Irvine




Phil 210 Logical Fallacy Logical Fallacy An Argument That Is Structurally Invalid Because Its Studocu



Is P Land P To Q To Q A Tautology Mathematics Stack Exchange




Some Other Logical Forms




Chapter 22 Common Propositional Argument Forms Introductory Remarks P 2 This Chapter Introduces Some Of The Most Commonly Used Deductive Argument Ppt Download




Logical Arguments Modus Ponens Modus Tollens Youtube
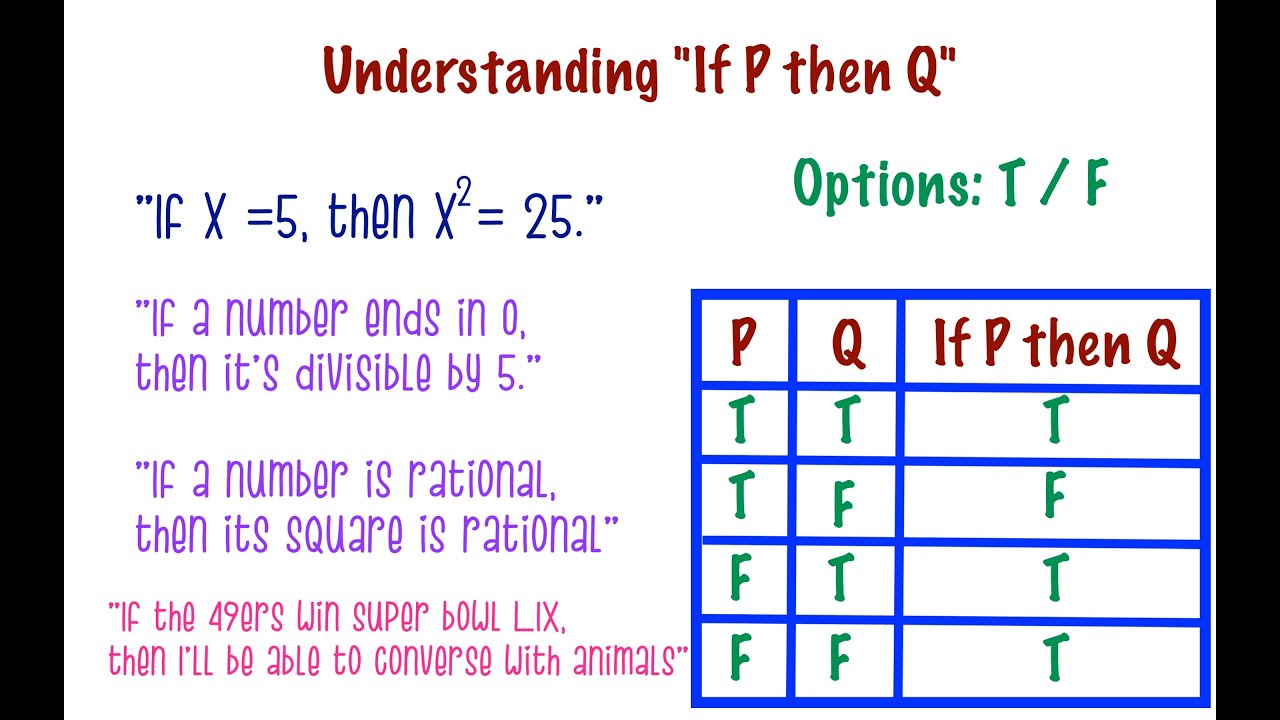



Understanding If P Then Q Youtube




Introduction To Philosophy Smu Fall 16 Tools




Apa Book Citation Examples Bibliography Com




Case Study Union Find




Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero




Critical Thinking Study Guide Study Guide Terms Antecedent The First Factor Upon Which The Studocu




In Praise Of Rationality The New York Times




Solved Which Of The Following Are Valid Logical Arguments Chegg Com



0 件のコメント:
コメントを投稿