
数字カードの組み合わせ 家庭学習レシピ
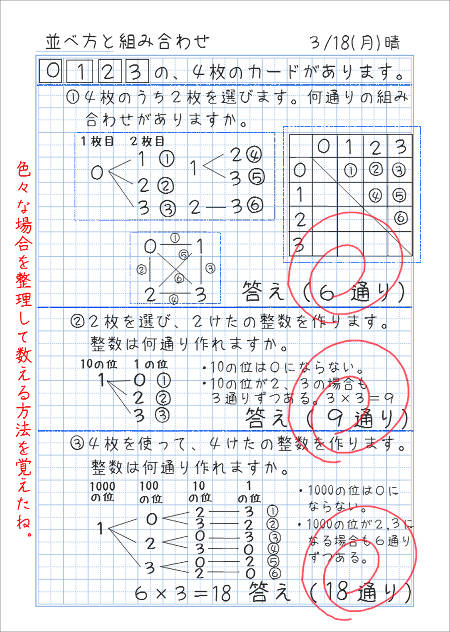
ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。順列の問題(ならべ方)1 (1)男子2人に女子3人でリレーの順番を決めます。 ①全部で何通りの順番がありますか。 ②男子と女子が交互になる順番は何通りありますか。 (2)0 1 2 3の4枚のカードから3枚を並べて3けたの整数を作ります。 ①全部で何通りの整数ができますか。
並べ方と組み合わせ方 問題
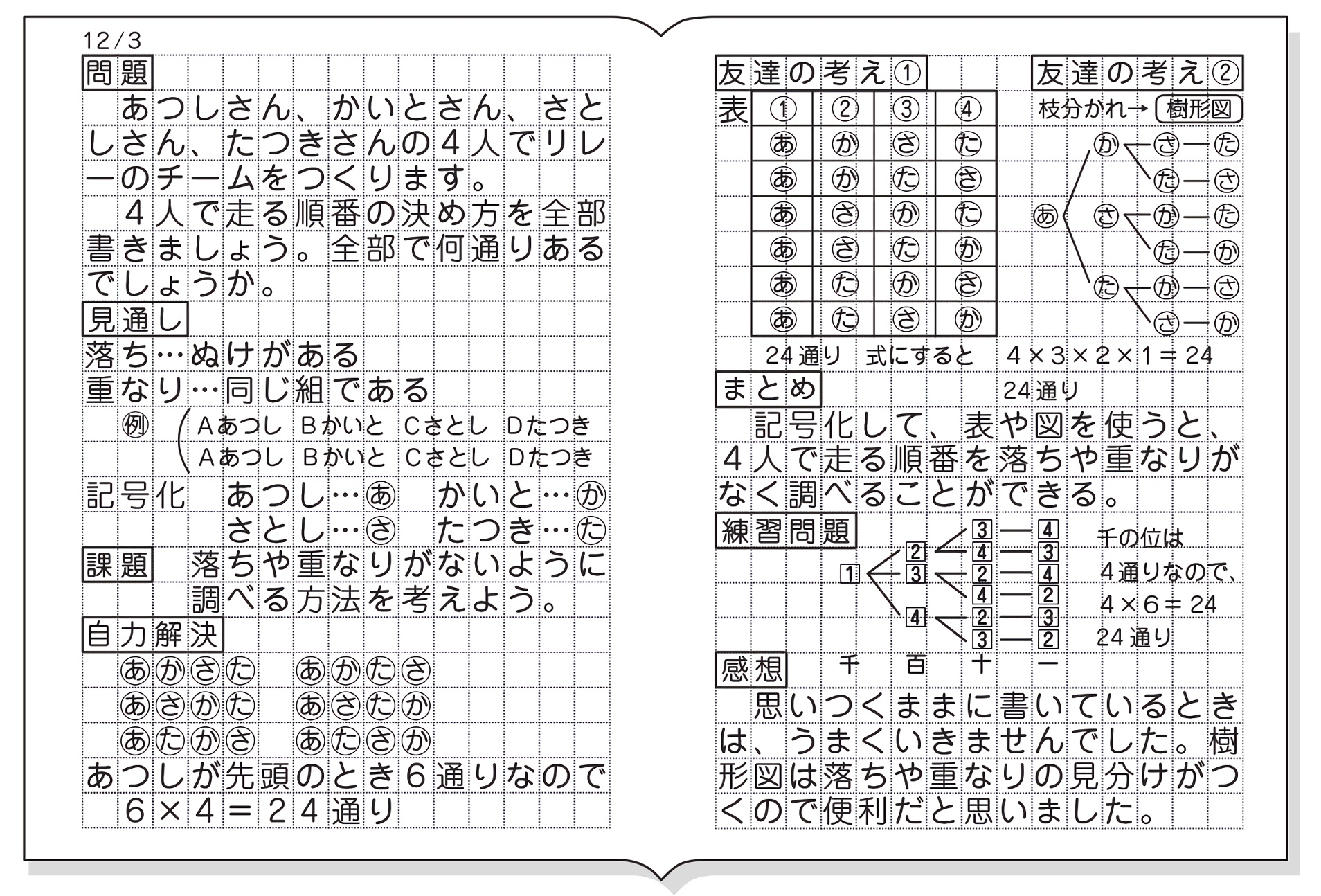
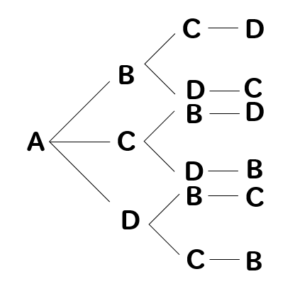
並べ方と組み合わせ方 問題-個順に並べるときの並べ方は全部で何通りあるか? 6P3 6u5u4 通り 10個の異なる文字(a,b,c,d,e,f,g,h,i,j) を,重複することな く,4個順に並べるときの並べ方は全部で何通りあるか? 10P4 10u9u8u7 通り n 個の異なる文字を,重複することなく,k個順に並べると 場合の数の順序を考えに入れた並べ方(順列)の問題です。 もれや重なりのないよう、順序よく図に表した樹形図を書いて考えます。 例)a,b,c,dの4枚のカードを1列に並べる 下のような図を書いて考えます。 aが1番目の図を

小学6年生の算数 動画 並べ方 組み合わせ方 の問題 19ch
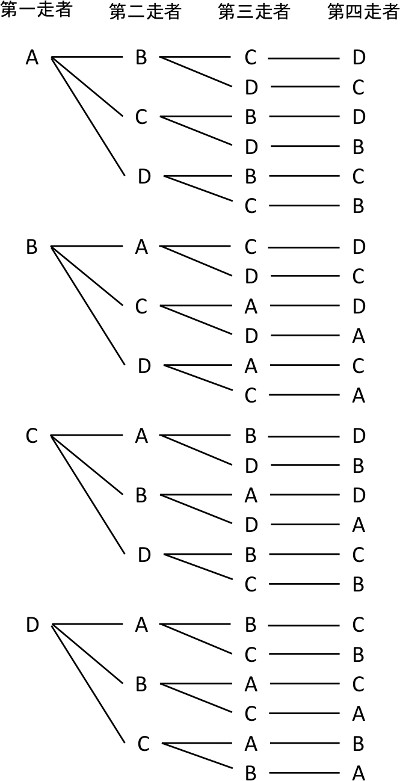
小学校 6年生 算数 かく力を高める問題 一括ダウンロード 文字と式 問題 分数のかけ算 問題 比 問題 角柱と円柱の体積 問題 並べ方と組み合わせ方 問題 データの調べ方 問題 たしかめ問題1 問題 たしかめ問題2 問題小学校 6年生 算数 かく力を高める問題 一括ダウンロード 文字と式 解答 分数のかけ算 解答 比 解答 角柱と円柱の体積 解答 並べ方と組み合わせ方 解答 データの調べ方 解答 たしかめ問題1 解答 たしかめ問題2 解答ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人
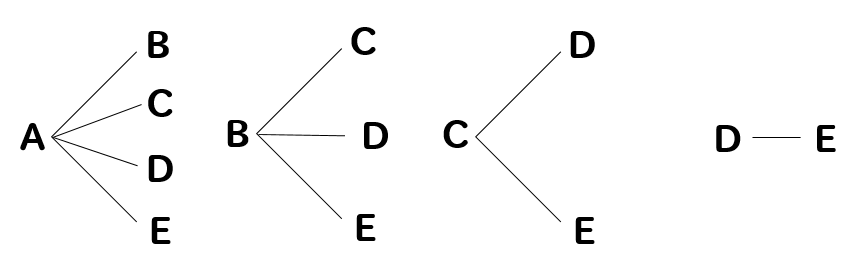
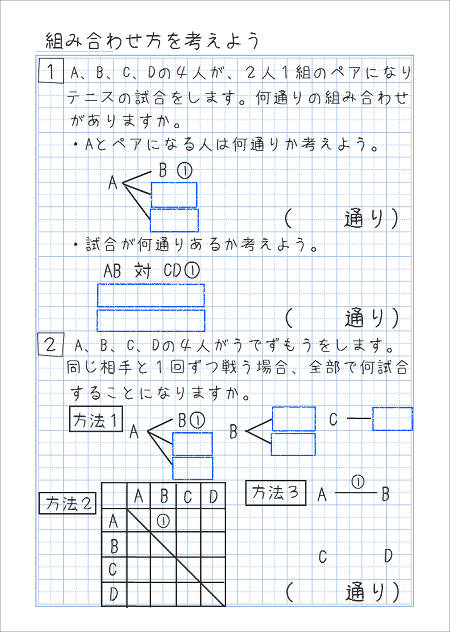
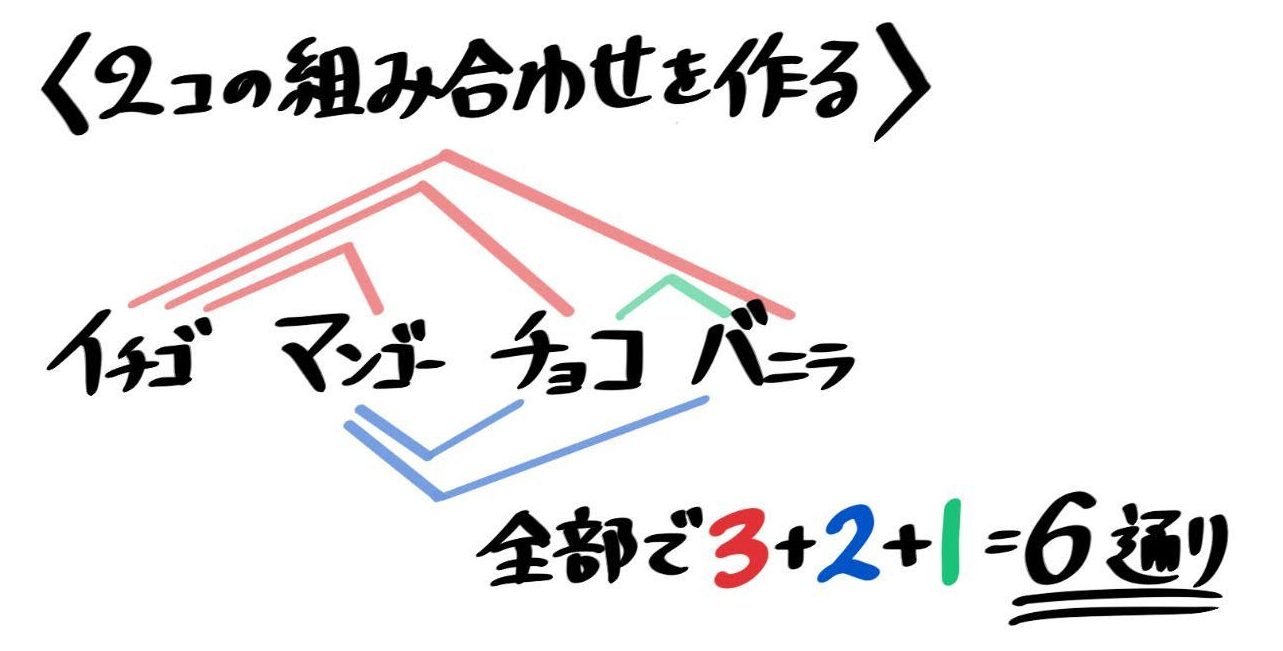
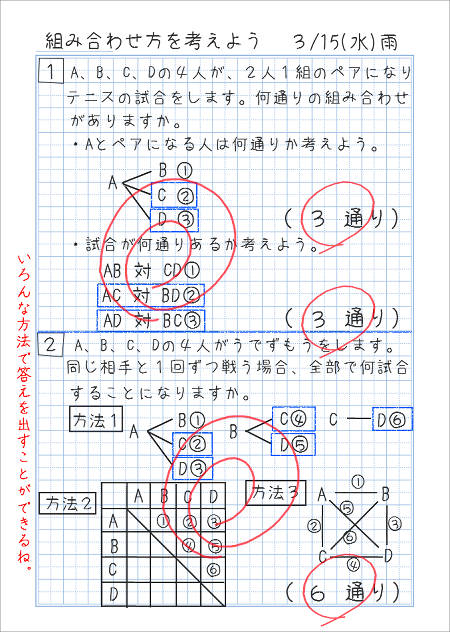
つまり、8個の要素のから3個を任意で取り出した時の並べ方は、何通りあるかという問題です。 手計算でいいのですが、ライブラリの pcipyを使うと簡単に計算できますね。 from scipyspecial import perm perm (8, 3, exact = True) 336 実装すると、336になります。 組み合わせの基本例)a,b,c,d,e の5人の中から2人ずつ組みになる作り方は何通りありますか。樹形図を書いて考える並べ方と違って ab 、ba は同じ組み合わせになるので、重ならないように書いて考えます。10通り計算で考える5×4=通り ←2人選ぶ並べ方ab と1 単元名 並べ方と組み合わせ方 2 単元について (1)単元観 本単元は、学習指導要領には以下のように位置づけられている。 目標 (d 数量関係) d(5)起こりえる場合
並べ方と組み合わせ方 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「並べ方と組み合わせ方 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
6年算数 並べ方と組み合わせ方 (場合の数)の教え方 6年算数「並べ方と組み合わせ方 (場合の数)」の教え方をわかりやすく紹介するサイトです。 保護者の方や先生方、学習支援ボランティアの方々の参考になれば幸いです。 12sansuujp このようなアニメで 重複組み合わせ 5 粒で考える 100 粒じゃなく、まず 5 粒という小さいスケールで考えてみます。 また「順序が問われない」なら、a, b, c と順序を固定して考える方がシンプルです。 これは「仕切りの置き場所の組み合わせ」の問題
Incoming Term: 並べ方と組み合わせ方 問題,




0 件のコメント:
コメントを投稿